Examples — Primal Simplex, Canonical Form of LP
Source:vignettes/examples_primal_simplex_1.Rmd
examples_primal_simplex_1.RmdStandard Case
— Werners, Brigitte - Grundlagen des Operations Research (p. 60)
\[ \begin{array}{rrcrcr} \max & 3x_1 & + & 2x_2 & \\ s.t. & 2x_1 & + & 1x_2 & \leq & 22 \\ & 1x_1 & + & 2x_2 & \leq & 23 \\ & 4x_1 & + & 1x_2 & \leq & 40 \\ & x_1,& & x_2 & \geq & 0 \end{array} \]
# standard case
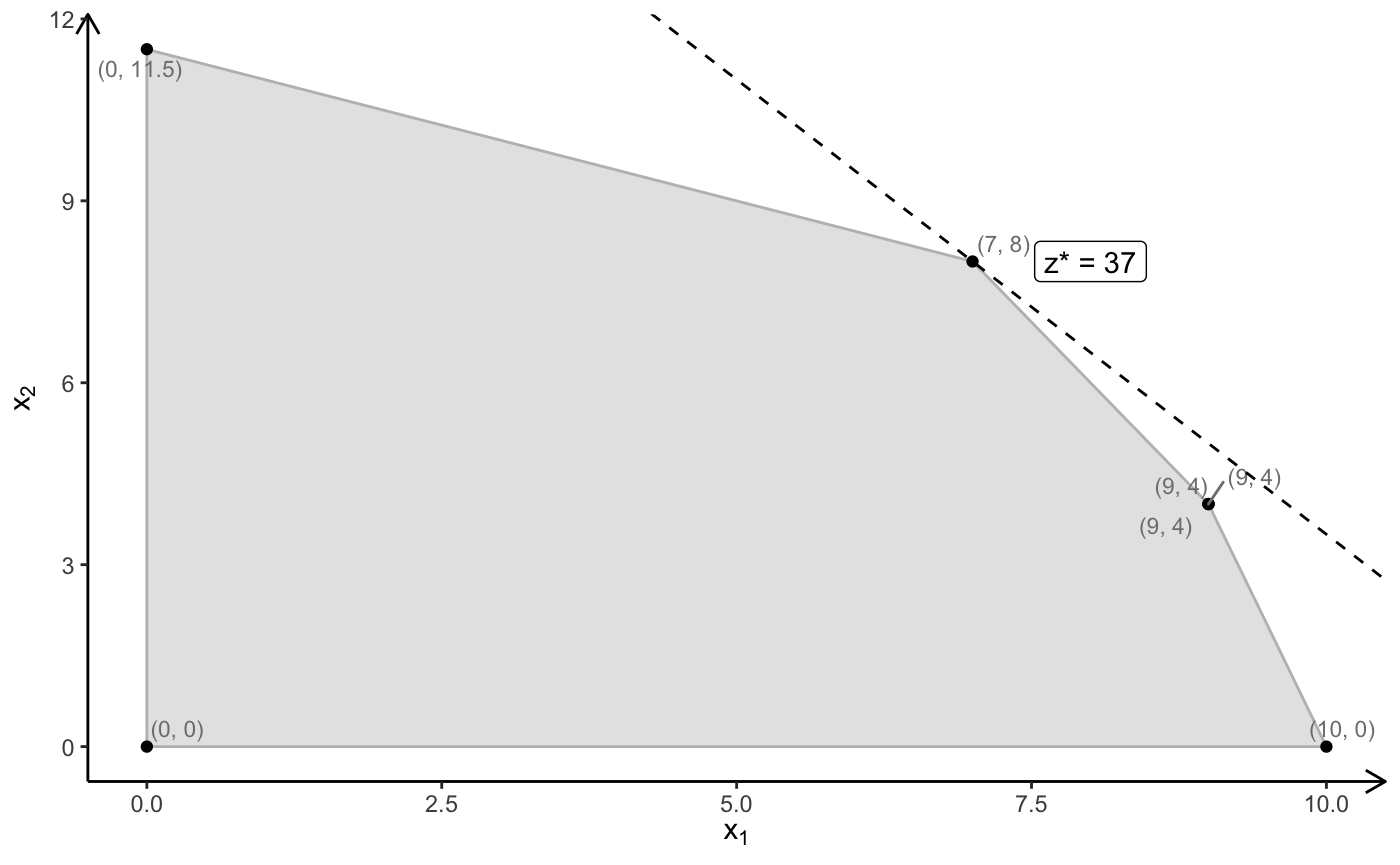
# optimal solution: x = (7, 8), z = 37
A <- matrix(c(
2, 1,
1, 2,
4, 1
), nrow = 3, ncol = 2, byrow = TRUE, dimnames = list(c("R1", "R2", "R3"), c("x1", "x2")))
b <- c(22, 23, 40)
c <- c(3, 2)
simplexR(A, b, c)## [1] "Start constructing Simplex Tableau"
## [1] "Tableau constructed"
## [1] "Initial Tableau (Tableau 0)"
## x1 x2 s s s b
## R1 2 1 1 0 0 22
## R2 1 2 0 1 0 23
## R3 4 1 0 0 1 40
## z -3 -2 0 0 0 0
## [1] "--------------------------------------------------------------------"
## [1] "Iteration 1"
## [1] "--------------------------------------------------------------------"
## [1] "Pivot column: 1"
## [1] "Pivot row: 3"
## [1] "New tableau at the end of iteration 1"
## x1 x2 s s s b
## R1 0 0.50 1 0 -0.50 2
## R2 0 1.75 0 1 -0.25 13
## R3 1 0.25 0 0 0.25 10
## z 0 -1.25 0 0 0.75 30
## [1] "--------------------------------------------------------------------"
## [1] "Iteration 2"
## [1] "--------------------------------------------------------------------"
## [1] "Pivot column: 2"
## [1] "Pivot row: 1"
## [1] "New tableau at the end of iteration 2"
## x1 x2 s s s b
## R1 0 1 2.0 0 -1.0 4
## R2 0 0 -3.5 1 1.5 6
## R3 1 0 -0.5 0 0.5 9
## z 0 0 2.5 0 -0.5 35
## [1] "--------------------------------------------------------------------"
## [1] "Iteration 3"
## [1] "--------------------------------------------------------------------"
## [1] "Pivot column: 5"
## [1] "Pivot row: 2"
## [1] "New tableau at the end of iteration 3"
## x1 x2 s s s b
## R1 0 1 -0.3333333 0.6666667 0 8
## R2 0 0 -2.3333333 0.6666667 1 4
## R3 1 0 0.6666667 -0.3333333 0 7
## z 0 0 1.3333333 0.3333333 0 37
## [1] "--------------------------------------------------------------------"
## [1] "Status: End"
## [1] "--------------------------------------------------------------------"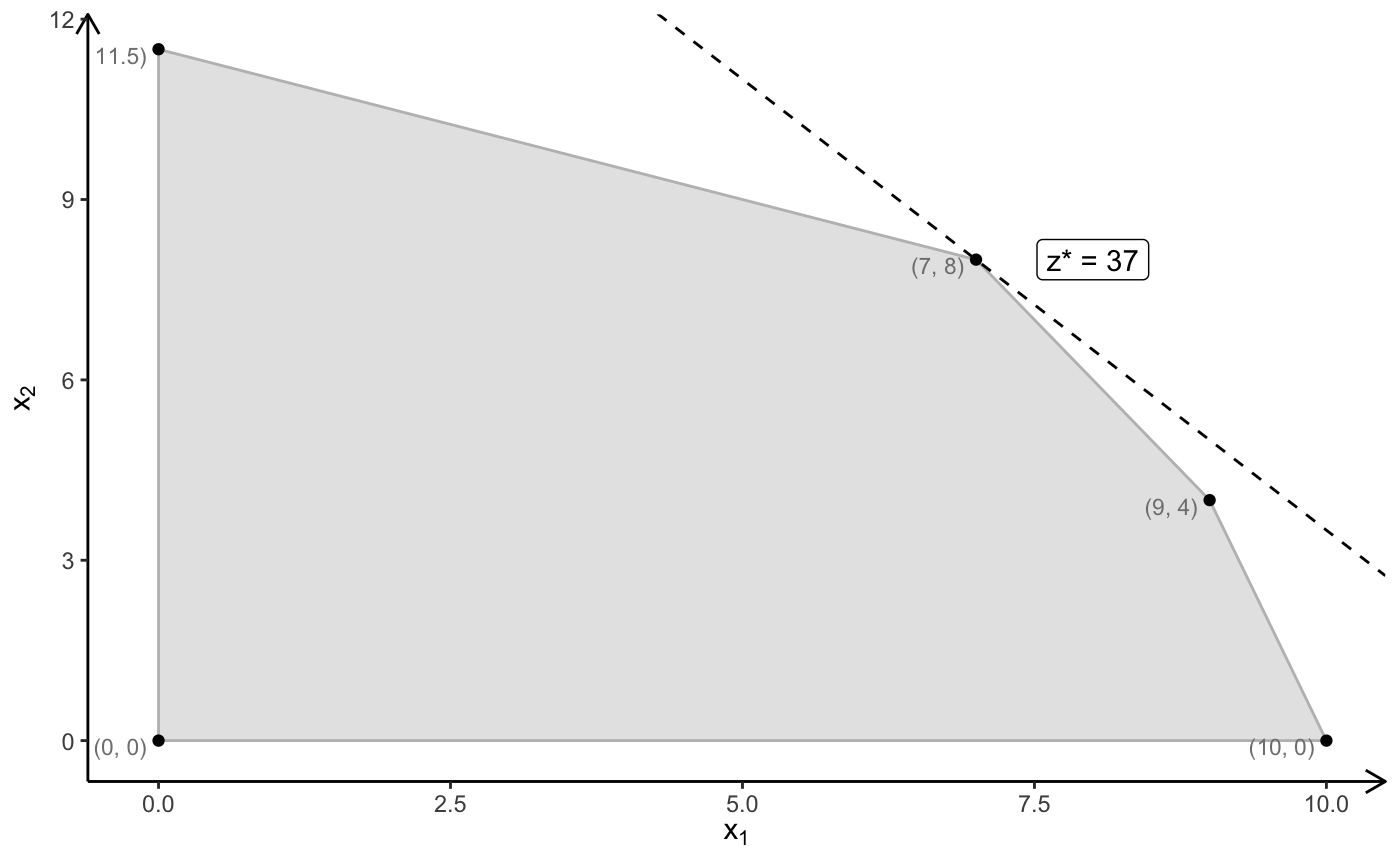
Standard Case—Exponential Time Complexity
\[ \begin{array}{rrcrcr} \max & 2x_1 & + & 1x_2 & \\ s.t. & 1x_1 & & & \leq & 5 \\ & 4x_1 & + & 1x_2 & \leq & 25 \\ & x_1,& & x_2 & \geq & 0 \end{array} \]
# standard case
# optimal solution: x = (0, 25), z = 25
A <- matrix(c(
1, 0,
4, 1
), nrow = 2, ncol = 2, byrow = TRUE, dimnames = list(c("R1", "R2"), c("x1", "x2")))
b <- c(5, 25)
c <- c(2, 1)
simplexR(A, b, c)## [1] "Start constructing Simplex Tableau"
## [1] "Tableau constructed"
## [1] "Initial Tableau (Tableau 0)"
## x1 x2 s s b
## R1 1 0 1 0 5
## R2 4 1 0 1 25
## z -2 -1 0 0 0
## [1] "--------------------------------------------------------------------"
## [1] "Iteration 1"
## [1] "--------------------------------------------------------------------"
## [1] "Pivot column: 1"
## [1] "Pivot row: 1"
## [1] "New tableau at the end of iteration 1"
## x1 x2 s s b
## R1 1 0 1 0 5
## R2 0 1 -4 1 5
## z 0 -1 2 0 10
## [1] "--------------------------------------------------------------------"
## [1] "Iteration 2"
## [1] "--------------------------------------------------------------------"
## [1] "Pivot column: 2"
## [1] "Pivot row: 2"
## [1] "New tableau at the end of iteration 2"
## x1 x2 s s b
## R1 1 0 1 0 5
## R2 0 1 -4 1 5
## z 0 0 -2 1 15
## [1] "--------------------------------------------------------------------"
## [1] "Iteration 3"
## [1] "--------------------------------------------------------------------"
## [1] "Pivot column: 3"
## [1] "Pivot row: 1"
## [1] "New tableau at the end of iteration 3"
## x1 x2 s s b
## R1 1 0 1 0 5
## R2 4 1 0 1 25
## z 2 0 0 1 25
## [1] "--------------------------------------------------------------------"
## [1] "Status: End"
## [1] "--------------------------------------------------------------------"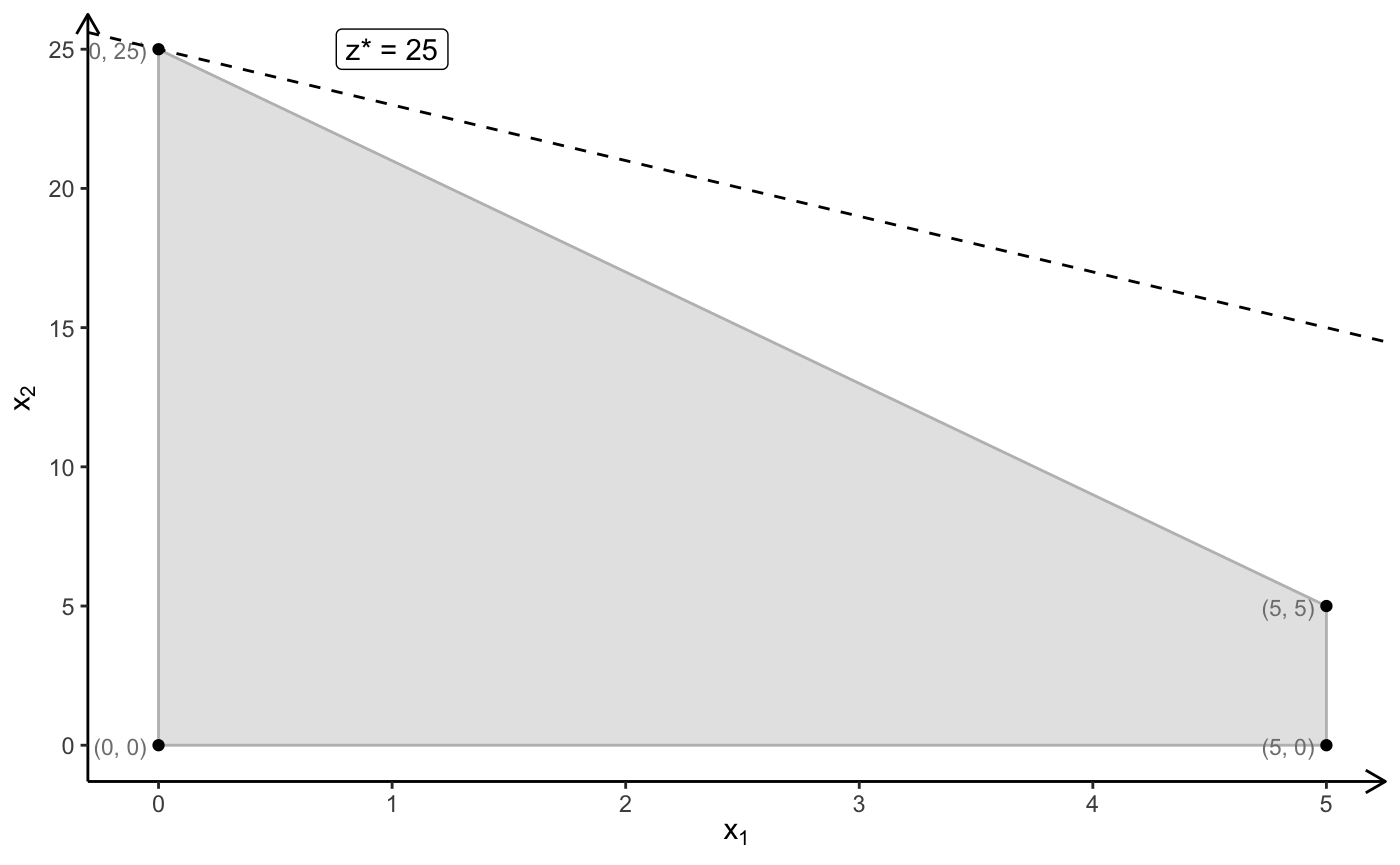
Unbounded Feasible Region, Optimal Solution
\[ \begin{array}{rrcrcr} \max &-2x_1 & + & 3x_2 & \\ s.t. &-1x_1 & + & 1x_2 & \leq & 2 \\ &-1x_1 & + & 2x_2 & \leq & 6 \\ & & & 1x_2 & \leq & 5 \\ & x_1,& & x_2 & \geq & 0 \end{array} \]
# unbounded feasible region, optimal solution exists
# optimal solution: x = (2, 4), z = 8
A <- matrix(c(
-1, 1,
-1, 2,
0, 1
), nrow = 3, ncol = 2, byrow = TRUE, dimnames = list(c("R1", "R2", "R3"), c("x1", "x2")))
b <- c(2, 6, 5)
c <- c(-2, 3)
simplexR(A, b, c)## [1] "Start constructing Simplex Tableau"
## [1] "Tableau constructed"
## [1] "Initial Tableau (Tableau 0)"
## x1 x2 s s s b
## R1 -1 1 1 0 0 2
## R2 -1 2 0 1 0 6
## R3 0 1 0 0 1 5
## z 2 -3 0 0 0 0
## [1] "--------------------------------------------------------------------"
## [1] "Iteration 1"
## [1] "--------------------------------------------------------------------"
## [1] "Pivot column: 2"
## [1] "Pivot row: 1"
## [1] "New tableau at the end of iteration 1"
## x1 x2 s s s b
## R1 -1 1 1 0 0 2
## R2 1 0 -2 1 0 2
## R3 1 0 -1 0 1 3
## z -1 0 3 0 0 6
## [1] "--------------------------------------------------------------------"
## [1] "Iteration 2"
## [1] "--------------------------------------------------------------------"
## [1] "Pivot column: 1"
## [1] "Pivot row: 2"
## [1] "New tableau at the end of iteration 2"
## x1 x2 s s s b
## R1 0 1 -1 1 0 4
## R2 1 0 -2 1 0 2
## R3 0 0 1 -1 1 1
## z 0 0 1 1 0 8
## [1] "--------------------------------------------------------------------"
## [1] "Status: End"
## [1] "--------------------------------------------------------------------"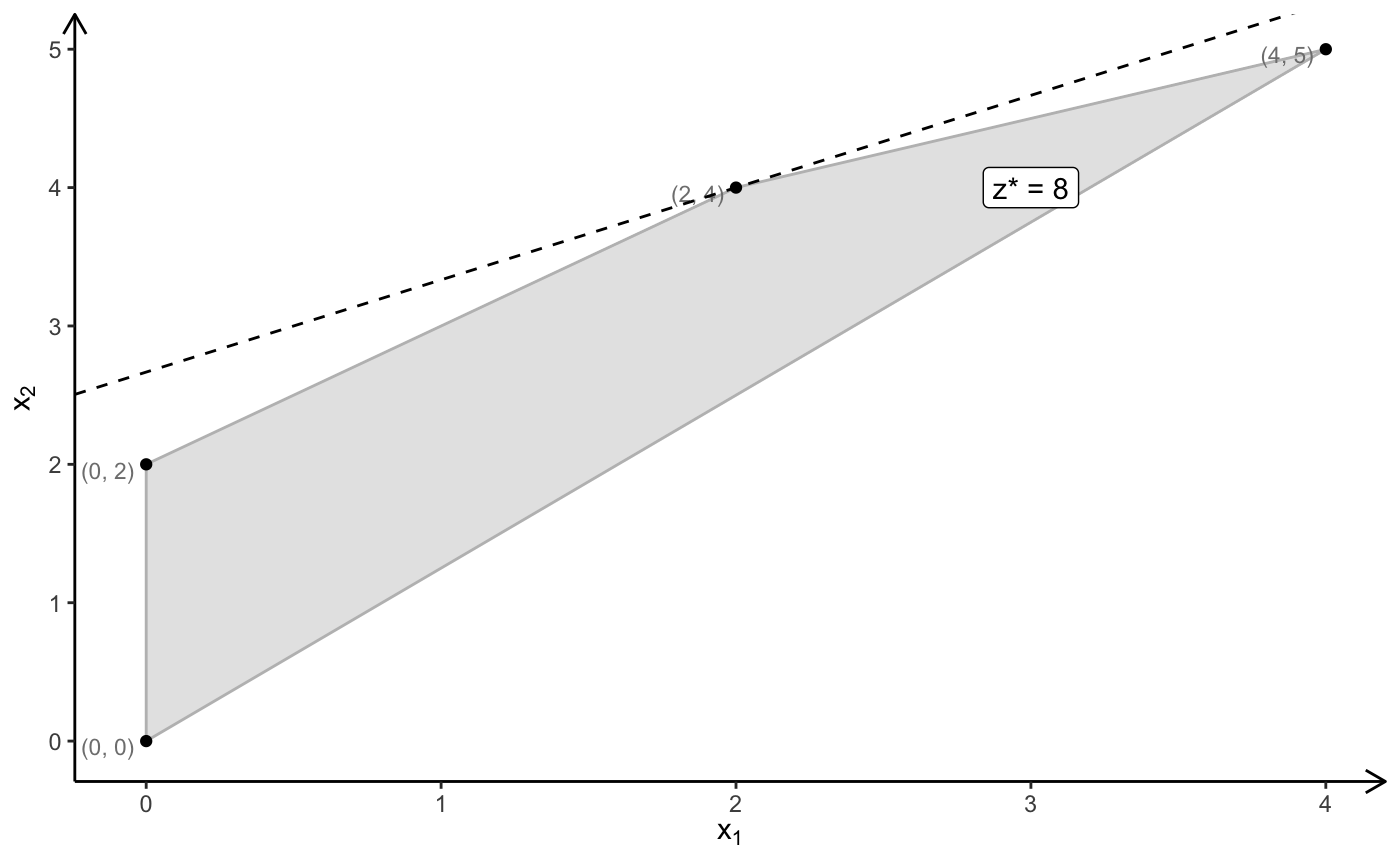
Unbounded Feasible Region, no Optimal Solution
— Werners, Brigitte - Grundlagen des Operations Research (p. 60)
\[ \begin{array}{rrcrcr} \max & 2x_1 & + & 4x_2 & \\ s.t. &-2x_1 & + & 3x_2 & \leq & 12 \\ &-1x_1 & + & 3x_2 & \leq & 18 \\ & x_1,& & x_2 & \geq & 0 \end{array} \]
# unbounded feasible region, no optimal solution exists
A <- matrix(c(
-2, 3,
-1, 3
), nrow = 2, ncol = 2, byrow = TRUE, dimnames = list(c("R1", "R2"), c("x1", "x2")))
b <- c(12, 18)
c <- c(2, 4)
simplexR(A, b, c)## [1] "Start constructing Simplex Tableau"
## [1] "Tableau constructed"
## [1] "Initial Tableau (Tableau 0)"
## x1 x2 s s b
## R1 -2 3 1 0 12
## R2 -1 3 0 1 18
## z -2 -4 0 0 0
## [1] "--------------------------------------------------------------------"
## [1] "Iteration 1"
## [1] "--------------------------------------------------------------------"
## [1] "Pivot column: 2"
## [1] "Pivot row: 1"
## [1] "New tableau at the end of iteration 1"
## x1 x2 s s b
## R1 -0.6666667 1 0.3333333 0 4
## R2 1.0000000 0 -1.0000000 1 6
## z -4.6666667 0 1.3333333 0 16
## [1] "--------------------------------------------------------------------"
## [1] "Iteration 2"
## [1] "--------------------------------------------------------------------"
## [1] "Pivot column: 1"
## [1] "Pivot row: 2"
## [1] "New tableau at the end of iteration 2"
## x1 x2 s s b
## R1 0 1 -0.3333333 0.6666667 8
## R2 1 0 -1.0000000 1.0000000 6
## z 0 0 -3.3333333 4.6666667 44
## [1] "--------------------------------------------------------------------"
## [1] "Iteration 3"
## [1] "--------------------------------------------------------------------"
## [1] "Pivot column: 3"
## [1] "Problem is unbounded -> stop execution"
## [1] "--------------------------------------------------------------------"
## [1] "Status: End"
## [1] "--------------------------------------------------------------------"Dual Degeneracy
— Werners, Brigitte - Grundlagen des Operations Research (p. 62)
\[ \begin{array}{rrcrcr} \max & 3x_1 & + &1.5x_2 & \\ s.t. & 2x_1 & + & 1x_2 & \leq & 22 \\ & 1x_1 & + & 2x_2 & \leq & 23 \\ & 4x_1 & + & 1x_2 & \leq & 40 \\ & x_1,& & x_2 & \geq & 0 \end{array} \]
# dual degeneracy
# optimal solution: x = (9, 4), z = 33
# optimal solution: x = (7, 8), z = 33
A <- matrix(c(
2, 1,
1, 2,
4, 1
), nrow = 3, ncol = 2, byrow = TRUE, dimnames = list(c("R1", "R2", "R3"), c("x1", "x2")))
b <- c(22, 23, 40)
c <- c(3, 1.5)
simplexR(A, b, c)## [1] "Start constructing Simplex Tableau"
## [1] "Tableau constructed"
## [1] "Initial Tableau (Tableau 0)"
## x1 x2 s s s b
## R1 2 1.0 1 0 0 22
## R2 1 2.0 0 1 0 23
## R3 4 1.0 0 0 1 40
## z -3 -1.5 0 0 0 0
## [1] "--------------------------------------------------------------------"
## [1] "Iteration 1"
## [1] "--------------------------------------------------------------------"
## [1] "Pivot column: 1"
## [1] "Pivot row: 3"
## [1] "New tableau at the end of iteration 1"
## x1 x2 s s s b
## R1 0 0.50 1 0 -0.50 2
## R2 0 1.75 0 1 -0.25 13
## R3 1 0.25 0 0 0.25 10
## z 0 -0.75 0 0 0.75 30
## [1] "--------------------------------------------------------------------"
## [1] "Iteration 2"
## [1] "--------------------------------------------------------------------"
## [1] "Pivot column: 2"
## [1] "Pivot row: 1"
## [1] "New tableau at the end of iteration 2"
## x1 x2 s s s b
## R1 0 1 2.0 0 -1.0 4
## R2 0 0 -3.5 1 1.5 6
## R3 1 0 -0.5 0 0.5 9
## z 0 0 1.5 0 0.0 33
## [1] "--------------------------------------------------------------------"
## [1] "Status: End"
## [1] "--------------------------------------------------------------------"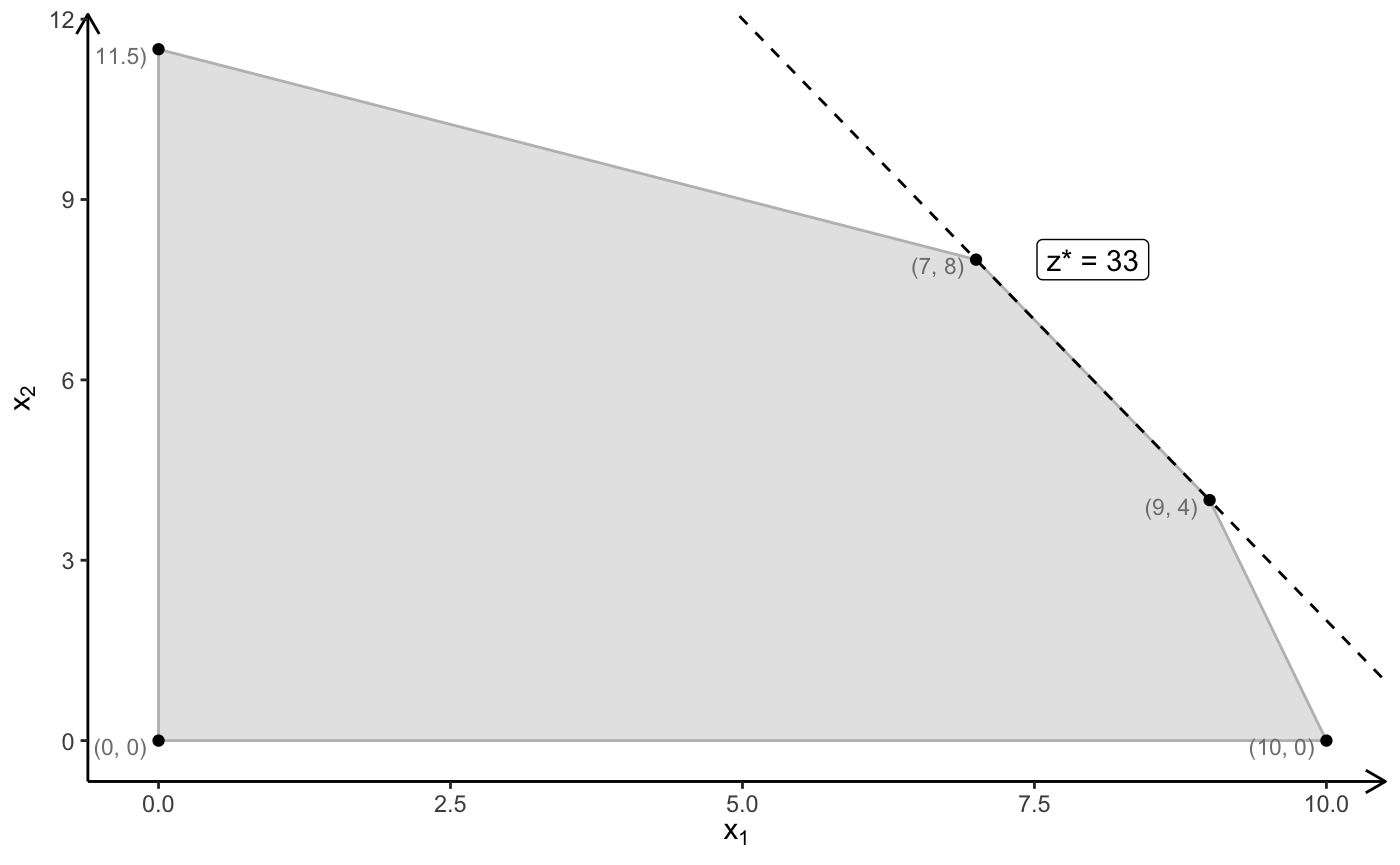
Primal Degeneracy
— Werners, Brigitte - Grundlagen des Operations Research (p. 65)
\[ \begin{array}{rrcrcr} \max & 3x_1 & + & 2x_2 & \\ s.t. & 2x_1 & + & 1x_2 & \leq & 22 \\ & 1x_1 & + & 2x_2 & \leq & 23 \\ & 4x_1 & + & 1x_2 & \leq & 40 \\ & 2x_1 & + & 0.75x_2 & \leq & 21 \\ & x_1,& & x_2 & \geq & 0 \end{array} \]
# primal degeneracy
# optimal solution: x = (7, 8), z = 37
A <- matrix(c(
2, 1,
1, 2,
4, 1,
2, 3/4
), nrow = 4, ncol = 2, byrow = TRUE, dimnames = list(c("R1", "R2", "R3", "R4"), c("x1", "x2")))
b <- c(22, 23, 40, 21)
c <- c(3, 2)
simplexR(A, b, c)## [1] "Start constructing Simplex Tableau"
## [1] "Tableau constructed"
## [1] "Initial Tableau (Tableau 0)"
## x1 x2 s s s s b
## R1 2 1.00 1 0 0 0 22
## R2 1 2.00 0 1 0 0 23
## R3 4 1.00 0 0 1 0 40
## R4 2 0.75 0 0 0 1 21
## z -3 -2.00 0 0 0 0 0
## [1] "--------------------------------------------------------------------"
## [1] "Iteration 1"
## [1] "--------------------------------------------------------------------"
## [1] "Pivot column: 1"
## [1] "Pivot row: 3"
## [1] "New tableau at the end of iteration 1"
## x1 x2 s s s s b
## R1 0 0.50 1 0 -0.50 0 2
## R2 0 1.75 0 1 -0.25 0 13
## R3 1 0.25 0 0 0.25 0 10
## R4 0 0.25 0 0 -0.50 1 1
## z 0 -1.25 0 0 0.75 0 30
## [1] "--------------------------------------------------------------------"
## [1] "Iteration 2"
## [1] "--------------------------------------------------------------------"
## [1] "Pivot column: 2"
## [1] "Pivot row: 1"
## [1] "New tableau at the end of iteration 2"
## x1 x2 s s s s b
## R1 0 1 2.0 0 -1.00 0 4
## R2 0 0 -3.5 1 1.50 0 6
## R3 1 0 -0.5 0 0.50 0 9
## R4 0 0 -0.5 0 -0.25 1 0
## z 0 0 2.5 0 -0.50 0 35
## [1] "--------------------------------------------------------------------"
## [1] "Iteration 3"
## [1] "--------------------------------------------------------------------"
## [1] "Pivot column: 5"
## [1] "Pivot row: 2"
## [1] "New tableau at the end of iteration 3"
## x1 x2 s s s s b
## R1 0 1 -0.3333333 0.6666667 0 0 8
## R2 0 0 -2.3333333 0.6666667 1 0 4
## R3 1 0 0.6666667 -0.3333333 0 0 7
## R4 0 0 -1.0833333 0.1666667 0 1 1
## z 0 0 1.3333333 0.3333333 0 0 37
## [1] "--------------------------------------------------------------------"
## [1] "Status: End"
## [1] "--------------------------------------------------------------------"