Examples — Revised Simplex Algorithm

In simplex method the entire simplex tableau is updated while a small part of it is used. The revised simplex method uses exactly the same steps as those in simplex method. The only difference occurs in the details of computing the entering variables and departing variable

— Werners, Brigitte - Grundlagen des Operations Research (p. 60)

\[ \begin{array}{rrcrcr} \max & 3x_1 & + & 2x_2 & \\ s.t. & 2x_1 & + & 1x_2 & \leq & 22 \\ & 1x_1 & + & 2x_2 & \leq & 23 \\ & 4x_1 & + & 1x_2 & \leq & 40 \\ & x_1,& & x_2 & \geq & 0 \end{array} \]

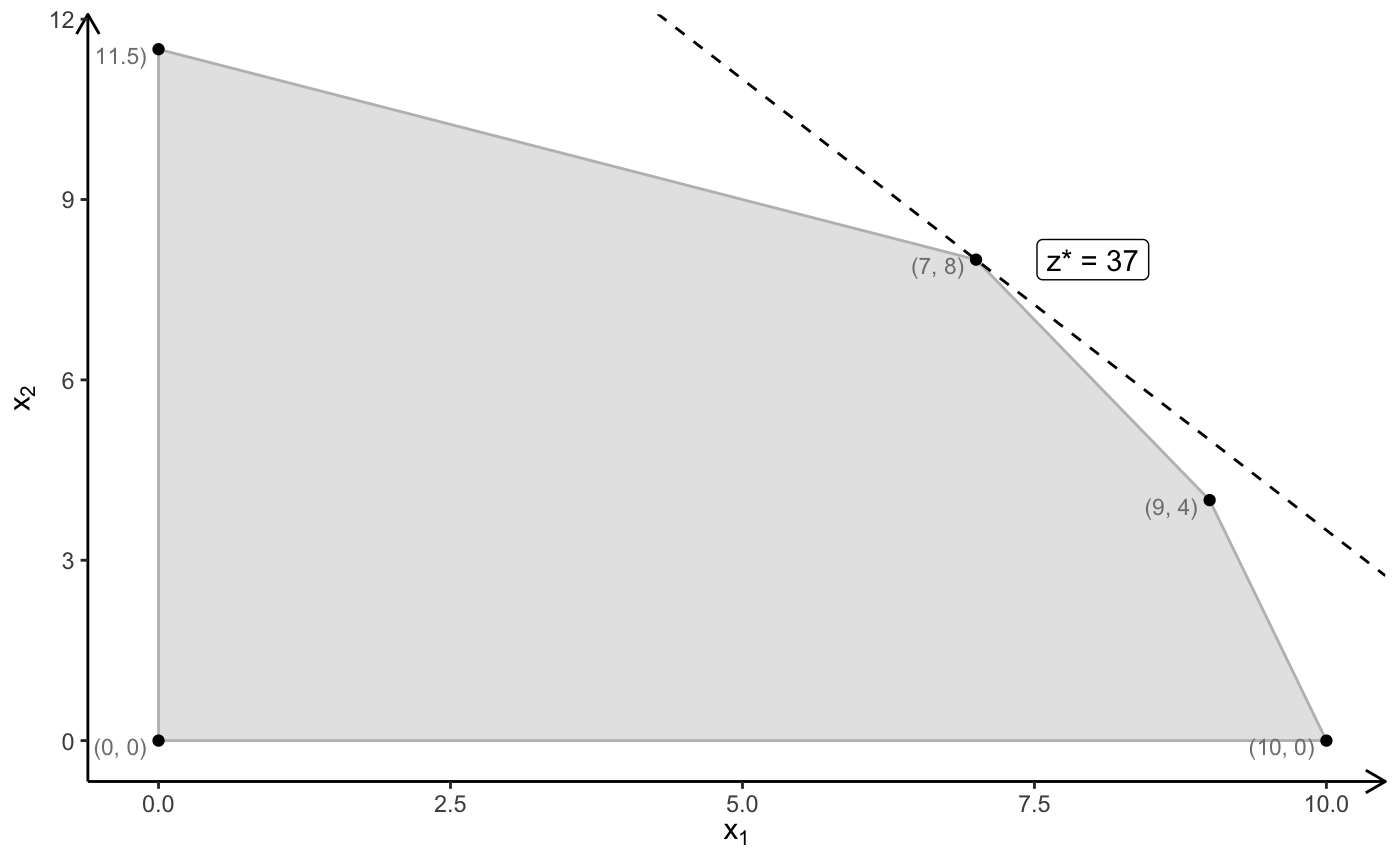
Tableau Form

A_ <- matrix(c(
  2, 1,
  1, 2,
  4, 1
), nrow = 3, ncol = 2, byrow = TRUE, dimnames = list(c("R1", "R2", "R3"), c("x1", "x2")))

b_ <- c(22, 23, 40)
c_ <- c(3, 2)

primal_feasible_tableau <- construct_tableau(A_, b_, c_)

## [1] "Start constructing Simplex Tableau"
## [1] "Tableau constructed"

primal_feasible_tableau

##    x1 x2 s s s  b
## R1  2  1 1 0 0 22
## R2  1  2 0 1 0 23
## R3  4  1 0 0 1 40
## z  -3 -2 0 0 0  0

Revised Simplex Algorithm

## optimal tableau:
##    x1 x2          s          s s  b
## R1  0  1 -0.3333333  0.6666667 0  8
## R2  0  0 -2.3333333  0.6666667 1  4
## R3  1  0  0.6666667 -0.3333333 0  7
## z   0  0  1.3333333  0.3333333 0 37

A <- cbind(A_, diag(nrow(A_)))
b <- b_
obj <- c(c_, rep(0, 3))
basic <- c(3, 4, 5)

revised_primal_simplex(A, b, obj, basic)

## [1] "Initialise"
## [1] "Initial Basis B"
## [1] 3 4 5
## [1] "Initial non-Basis N"
## [1] 1 2
## [1] "------------------------------------------------------------------------------------"
## [1] "Iteration 1"
## [1] "delta c = "
##      x1 x2
## [1,] -3 -2
## [1] "position of min in non-Basis = 1"
## [1] "Pivot column = 1"
## [1] "New basis B"
## [1] 3 4 1
## [1] "New non-basis after iteration N"
## [1] 5 2
## [1] "basic feasible solution (BFS)"
##    [,1]
##       2
##      13
## x1   10
## [1] "End of iteration 1"
## [1] "------------------------------------------------------------------------------------"
## [1] "Iteration 2"
## [1] "delta c = "
##              x2
## [1,] 0.75 -1.25
## [1] "position of min in non-Basis = 2"
## [1] "Pivot column = 2"
## [1] "New basis B"
## [1] 2 4 1
## [1] "New non-basis after iteration N"
## [1] 5 3
## [1] "basic feasible solution (BFS)"
##    [,1]
## x2    4
##       6
## x1    9
## [1] "End of iteration 2"
## [1] "------------------------------------------------------------------------------------"
## [1] "Iteration 3"
## [1] "delta c = "
##              
## [1,] -0.5 2.5
## [1] "position of min in non-Basis = 1"
## [1] "Pivot column = 5"
## [1] "New basis B"
## [1] 2 5 1
## [1] "New non-basis after iteration N"
## [1] 4 3
## [1] "basic feasible solution (BFS)"
##    [,1]
## x2    8
##       4
## x1    7
## [1] "End of iteration 3"
## [1] "------------------------------------------------------------------------------------"
## [1] "Iteration 4"
## [1] "delta c = "
##                        
## [1,] 0.3333333 1.333333
## [1] "position of min in non-Basis = 1"
## [1] "Pivot column = 4"
## [1] "Optimal basic feasible solution found!"
## [1] "Optimal solution value z = 37"
## [1] "End"